The starting point of TGD is the 'energy problem' of General Relativity. By Noether's theorem, conservation laws are in one-one correspondence with symmetries. In particular, translational invariance of the empty Minkowski space M^4 implies energy and momentum conservation in Special Relativity. By the basic postulate of General Relativity matter makes spacetime curved. This means that the symmetries of the empty Minkowski space are lost as are lost also the corresponding conservation laws, in particular the conservation of energy.

The basic idea of TGD is to assume that spacetime is representable as a surface of some higher dimensional space H=M^4xS and that translational symmetries, and more generally, Poincare invariance correspond to the symmetries of M^4-factor of this higher-dimensional space rather than those of spacetime itself. Hence a fusion of Special and General Relativities in a well defined sense is in question. In fact mathematical and physical reasons force to replace empty Minkowski space M^4 with its light cone M^4_+. Future light cone corresponds to empty Robertson Walker cosmology and TGD inspired cosmology has subcritical mass density as a consequence. There is small cosmological breaking of Poincare invariance since M^4 is replaced by its lightcone.

Fig. 1. Matter makes spacetime curved and spoils translational invariance. Two-dimensional illustration.

By physical constraints (elementary particle spectrum) the space S must be CP_2, the complex projective space of two complex (four real) dimensions. The size of CP_2 is about 10^4 Planck lengths (roughly 10^(-30) meters). [It took long time to realize that the original assumption about size of order Planck length was not correct].

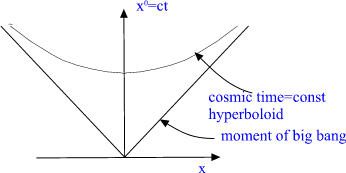
Fig. 2. Future light cone of Minkowski space.

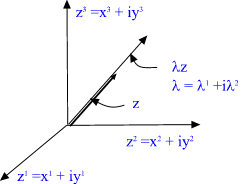
Fig. 3. CP2 is obtained by identifying all points of C^3, space having 3 complex dimensions, which differ by a complex scaling Lambda: z is identified with Lambda*z.

CP2 can also be regarded as a coset space SU(3)/U(2), U(2)=SU(2)xU(1). What this means is that one starts from the 8-dimensional group SU(3) of unitary 3x3 matrices of determinant one and identifies all matrices which differ by a left multiplication by an element of the 4-dimensional subgroup U(2). One can also say that each point of SU(3) is obtained from CP2 by replacing each point of CP2 with the group U(2). U(2) in turn can be regarded as S^3xS^1, that is as the space obtained by replacing each 2-dimensional disk giving a cross section of the ordinary torus (doughnut) with a 3-dimensional sphere S^3. By this construction CP2 is so called symmetric space, whose all points are equivalent metrically (like those of Euclidian space) and has color group SU(3) as its group of distance preserving transformations, isometries.

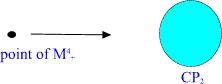
Fig. 4. H= M^4_+xCP_2 is obtained by replacing each point of the future light cone with the 4-dimensional compact space CP_2 of size R of order 10^4 Planck lengths (10^(-30) meters).

The second manner to end up with TGD is to start from the old fashioned string model, which also served as a starting point of super string models, which have been in fashion during the last ten years.

Mesons are strongly interacting particles and string model description was in terms of a string with quark and antiquark attached to the ends of the string. A problem was encountered in an attempt to generalize this description to apply to baryons which consist of three quarks. One cannot put 3 quarks to the ends of the string since it has only two ends.

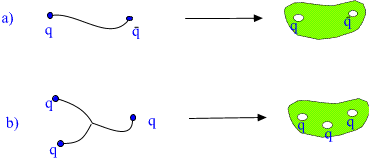
Fig. 5. The transition from hadronic string model to TGD.

The solution of the problem is simple. Replace one-dimensional strings with small 3-dimensional surfaces. Since the ends of the string correspond to the boundaries of a one-dimensional manifold they correspond in 3-dimensional case boundaries of small holes drilled in 3-dimensional space. Put quarks on these boundaries. In 3-dimensional case one can drill arbitrary number of these holes so that also baryons can be described in this kind of model.

TGD based spacetime concept differs in many crucial aspects from the conventional one. In the following this difference is visualized by replacing 3-dimensional space (now surface in H) with two-dimensional surface whereas 8-dimensional imbedding space is replaced with 3-dimensional slab of thickness of order 10^4 Planck lengths. This simplification makes it possible to illustrate the most essential aspects of the generalization easily and at least geometrically/topologically oriented reader can guess the rest.

Below is a general view of what many-sheeted 3-space would look like if it were 2-dimensional

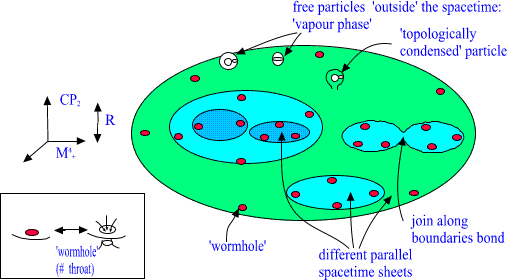
Fig. 6. This is what 3-space would look if it were a 2-dimensional surface in 3-dimensional slab of thickness of order 10^4 Planck lengths.

B. Elementary particles as 3-surfaces of size of order R=10^4 Planck lengths: CP2 extremals.

Elementary particles have geometric representation as so called CP2 type extremals. Instead of standard imbedding of CP2 as a surface of M^4+xCP2 obtained by putting Minkowski coordinates m^k constant

m^k=const.,

one considers 'warped' imbedding

m^k =f^k(u) u is arbitrary function of CP2 coordinates with the property that the M4_+ projection of the surface is random light like curve:

mkl dm^k/du dm^l/du =0, mkl is flat M4 metric. (A)

The condition implies that induced metric is just CP2 metric, which is Euclidian! The curve is random and therefore one has classical nondetermism: this makes sense since the solution is vacuum extremal.

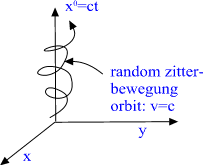
Fig. 7. The projection of CP2 type extremal to M4+ is lightlike curve.

Elementary particles correspond to CP2 type extremals with holes: the intersection of bound with m^0=const hyperplane is sphere, torus, sphere with two handles, etc...: shortly a surface with genus g=0,1,2,... . Different fermion families correspond to different genera. Bosons are also predicted to have family replication phenomenon.

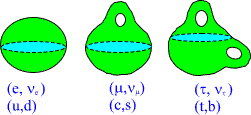
Fig. 8. Different fermion families correspond to different genera for the boundary component of CP2 type extremal.

Feynmann diagrams correspond to topological sums of CP2 type extremals: the lines of diagram being thickened to CP2 type extremals:

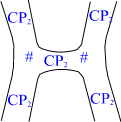
Fig. 9. Feynmann diagrams correspond to connected sums of CP2 type extremals: each line of Feynmann diagram is thickened to CP2 type extremal.

The quantum version of the condition (A) stating that the M4_+ projection is light like curve leads to Super Virasoro conditions and it turns out that elementary particles together with their 10^(-4) Planck mass excitations belong to representation of p-adic Super Virasoro and Kac Moody. The p-adic mass calculations lead to excellent predictions for particle masses.

C. Induced gauge field concept implies radical generalization of spacetime concept

The concept of connection geometrizes the concept of the parallel translation appearing already in elementary geometry. Parallel translation can be performed for vectors, tensors, spinors,... In Euclidian case parallel translation is just what one would imagine it to be and the parallel translation around a closed curve brings the vector back without any change in its direction. The formal definition of the parallel translation along a geodesic line (the counterpart of a straight line) in a more general context requires that the angle between the vector and geodesic line is preserved. Sphere is a simple example of a situation in which parallel translation around a closed curve changes the direction of the vector. One says that sphere is curved and curvature is locally measured by the amount of change in the direction of a vector for very small geodesic triangle.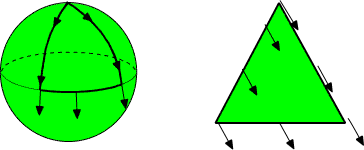

Fig. 10. Parallel translation on sphere and on plane.

In General Relativity, the so called Riemann connection defining the parallel translation in spacetime leads to a beautiful geometrization of the gravitational interaction. The presence of matter makes spacetime curved and geodesics are not straight lines anymore. The advent of the gauge theories led to a partial geometrization of the boson fields. The components of the gauge potentials can be regarded as components of a connection defining parallel translation formally.

The problem is however that there is not direct geometric interpretation for this parallel translation and here TGD provides the final geometrization of classical gauge field concept. The components of electroweak gauge potentials are obtained as projections of the spinor connection of CP2 to spacetime surface:

Amu = A_k partialmu h^k
(mu is the coordinate index for spacetime coordinates, k for imbedding space coordinates)

or geometrically; parallel translation on spacetime surface is performed using spinor connection of the imbedding space.

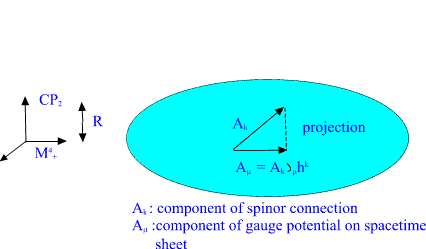
Fig. 11. Classical electroweak gauge potentials at spacetime surface are obtained as projections of the components of CP2 spinor connection.

Classical color gauge potentials are identified as projections of Killing vector fields of su(3) to spacetime surface (very much like in Kaluza-Klein theories). The requirement that standard model electroweak gauge group allows only M^4_+xCP2 as imbedding space. Also standard model quantum numbers are geometrized in terms of CP2 geometry and topology of the boundary component of CP2 type extremal. The special features of CP2, in particular the fact that it does not allow standard spinor structure, are crucial for obtaining the coupling structure of standard model.

The induced gauge field concept differs from the ordinary one. The PRIMARY dynamical variables are the four CP2 coordinates and this implies strong constraints among classical gauge fields: for instance classical electric field is often accompanied by classical Z0 field even in macroscopic length scales.

There is rather precise metaphor making possible to understand the concept of induced gauge field intuitively. The shadow (projection!) of a nondynamical solid object ( < --> metric and spinor connection of H) with time-independent size and shape to a surface (<--> 3-surface) changing its size and shape is dynamical .

Fig. 12. Classical electroweak gauge potentials at spacetime surface are obtained as projections of the components of CP2 spinor connection.

Even more importantly: gauge potentials are determined by the image of map

X^4--> CP2

whereas ordinary gauge potentials are determined by the map

X^4 --> TM^4,

where TM^4 is the space of field values at given point of spacetime and isomorphic to tangent space of M4. CP2 is COMPACT whereas TM^4 is NONCOMPACT: a crucial difference!

This implies that general electromagnetic gauge potentials are imbeddable only in some open region surrounding given point of spacetime and that the imbeddability fails at the boundary of this region.

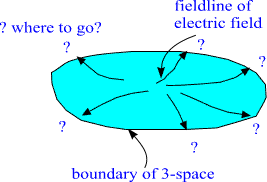
Fig. 13. The Maxwell field associated with a given charge distribution is representable as induced gauge field only in a finite region of spacetime. This implies the presence of boundaries. Two-dimensional illustration.

The failure of imbeddability leads to generation of spacetime BOUNDARIES in all lengths scales. At the boundary spacetime simply ends.

There is following problem on the boundaries: Kähler electric gauge flux must be conserved on the boundary. Since the 3-space ends at boundary there is no other manner to cope with situation than to introduce second, larger, spacetime sheet parallel to the first one and allow the gauge flux to run on this spacetime sheet via tiny wormholes connecting the two sheets. Wormhole is constructed by drilling tiny spherical holes inside the two parallel spacetime sheets and connecting the boundaries S^2 of the holes with a cylinder S^2 xI having two ends with S^2 topology. The figure below illustrates the situation if 3-space were two-dimensional.

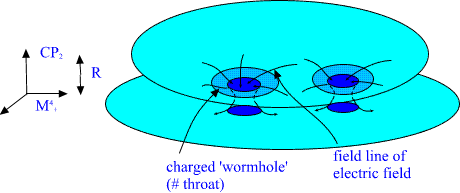
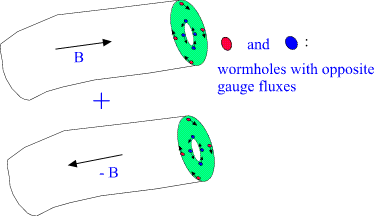
Fig. 14. Charged wormholes feed the electromagnetic gauge flux to the 'lower' spacetime sheet.

By adding these wormholes on the boundary of 3-surfaces the gauge flux can flow to the lower spacetime sheet. An interesting possibility is that wormholes are itself slightly deformed pieces of CP2 type extremals.

The throats of wormhole behave as classical charges -Q and Q , where Q is the electric gauge flux flowing to the wormhole at upper spacetime sheet and out of it at lower spacetime sheet. Thus they serve as currents and sources (of opposite sign) of classical gauge fields at the two spacetime sheets.

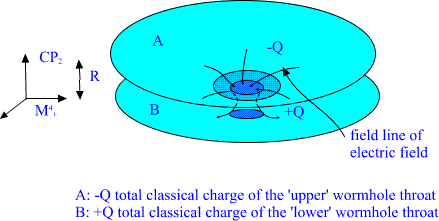
Fig. 15. The two throats of wormhole behave as classical charges of opposite sign.

Wormholes couple to the DIFFERENCE OF CLASSICAL GAUGE POTENTIALS associated with the two spacetime sheets since the classical charges are opposite.

It seems safe to assume that photons (the extremely small CP2 type extremals!) see wormholes from wider perspective that is extremely small dipoles formed by the throats. The distance between charges is of order 10^4 Planck lengths and the direction of dipole is transversal to spacetime surface so that polarization vector has very small projection in M^4, where polarization vector of photon is. Thus the coupling to photons should be negligible (dipole moment satisfies p > Q*R, R the size of CP_2, and thus also dissipation effects.

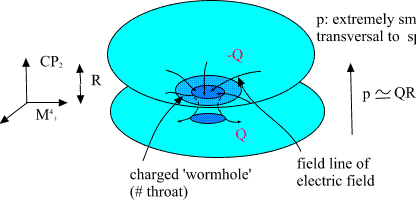
Fig. 16. As for as coupling to photons is considered wormoholes are expected to behave as extremely tiny dipoles.

This suggests very stronly that wormholes behaves much like conduction electrons and are thus localized to the boundaries of spatime surface. If wormholes are light (as they turn out to be) they obey d'Alembert type equation and there is large energy gap between ground state and excited states. Thus wormholes become suffer BE condensation to ground state: charged wormholes behave thus much like super-conductors.

Wormholes can have several topologies: in general one can drill holes of genus g (sphere, torus, etc...) on two spacetime sheets and connect them using cylinder I+genus g surface. In this they resemble ordinary elementary particles which have also several genera (family replication phenomenon).

The gauge flux conservation problem is encountered also in the lower spacetime sheet and one must introduce third, fourth, etc. spacetime sheet and in general one has hierarchy of spacetime sheets with increasing sizes.

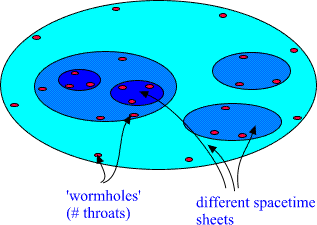
Fig. 17. Many sheeted spacetime structure results from the requirement of gauge flux conservation.

The conclusion is that induced gauge field concept leads unavoidably to the concept of many sheeted spacetime. This has radical consequences for the structure of physical theory: one must replace thermodynamics, hydrodynamics, etc with a hierachy of dynamics of various types, one for each spacetime sheet in the hierarchy. This replacement must be performed in ALL length scales.

D. Matter as topology

Since many sheetedness is encountered in all length scales a very attractive manner to reinterpret our visual experience about world suggests itself. Material objects having macroscopic boundaries correspond actually to sheets of 3-space and 3-space literally ends at the boundary of object. The 3-space outside the object corresponds to the 'lower' spacetime sheet. Actually we can see this wild 3-topology every moment!! The following 2-dimensional illustration should make clear what the generalization really means.

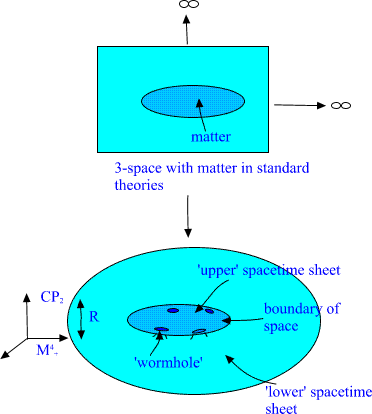
Fig. 18. Matter as topology

E. Join along boundaries contacts and join along boundaries condensate

The receipe for constructing many-sheeted 3-space is simple. Take 3-surfaces with boundaries, glue them by topological sum to larger 3-surfaces, glue these 3-surfaces in turn on even larger 3-surfaces, etc.. The smallest 3-surfaces correspond to CP2 type extremals that is elementary particles and they are at the top of hierachy. In this manner You get quarks, hadrons, nuclei, atoms, molecules,... cells, organs, ..., stars, ..,galaxies, etc...

Besides this one can also glue different 3-surfaces together by tubes connecting their BOUNDARIES : this is just connected sum operation for boundaries. Take disks D^2 on the boundaries of two objects and connect these disks by cylinder D^2xD1 having D^2:s as its ends. Or more concretely: let the two 3-surfaces just touch each other.

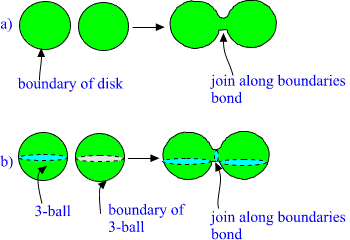
Fig. 19. Join along boundaries bond a): in two dimensions and b): in 3-dimensions for solid balls.

Depending on the scale join along boundariers bonds are identified as color flux tubes connecting quarks, bonds giving rise to strong binding between nucleons inside nuclei, bonds connecting neutrons inside neutron star, chemical bonds between atoms and molecules, gap junctions connecting cells, the bond which is formed when You touch table with Your finger, etc.

One can construct from a group of nearby disjoint 3-surfaces so called join along boundaries condensate by allowing them to touch each other here and there.

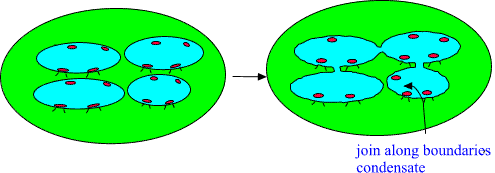
Fig. 20. Join along boundaries condensate in 2 dimensions.

The formation of join along boundaries condensates creates clearly strong correlation between two quantum systems and it is assumed that the formation of join along boundaries condensate is necessary prequisite for the formation of MACROSCOPIC QUANTUM SYSTEMS.

F. p-Adic numbers and vacuum degeneracy

p-Adic length scale hypothesis derives from the analogy between SPIN GLASS and TGD. Kähler action allows enormous VACUUM DEGENERACY: ANY spacetime surface, which belongs to M^4_+xY^2, where Y^2 is so called Legendre submanifold of CP2 is vacuum due to the vanishing of induced Kähler form (recall that Kähler action is just Maxwell action for induced Kähler form which can be regarded as U(1) gauge field).

Legendre submanifolds can be written in the canonical coordinates P^i,Q^i, i=1,2 for CP2 as

P^i =f^i(Q^1,Q^2)

f^i =partial_i f(Q^1,Q^2)

where partial_i means partial derivative with respect to Q^i. f is arbitrary function of Q^i! Legendre submanifolds are 2-dimensional. The topology of vacuum space time is restricted only by the imbeddability requirement. Vacuum spacetimes can have also finite extend in time direction(!!): charge conservation does not force infinite duration.

Fig. 21. Vacuum extremals can have finite time duration.

This enormous vacuum degeneracy resembles the infinite ground state degeneracy of spin glasses. In case of spin glasses the space of free energy minima obeys ultrametric topology. This raises the question whether the effective topology of the real spacetime sheets could be also ultrametric in some length scale range so that the distance function would satisfy

d(x,y) <= Max(d(x),d(y)) rather than d(x)+d(y)

p-Adic topologies are ultrametric and there is p-adic topology for each prime p=2,3,5,7,... The classical non-determinism of the vacuum extremals implies also classical non-determinism of field equations (but not complete randomness of course).

p-Adic differential equations are also inherently non-deterministic. This suggests that the non-determinism of Kähler action is effectively like p-adic non-determinism in some length scale range, so that that the topology of the real space-time sheet is effectively p-adic for some value p. The lower cutoff length scale could be CP_2 length scale. Of course, cutoff length scales could be dynamical.

Standard representation of p-adic number is defined as generalization of decimal expansion

x= SUM_(n>=n0) x_np^n

p-Adic norm reads as

N(x)_p = p^(-n0) ,

and clearly depends on the lowest pinary digit only and is thus very rough: for reals norm is same only for x and -x. Note that integers which are infinite as real numbers are finite as p-adic numbers: p-adic norm of any integer is at most one.

Essential element is the so called CANONICAL CORRESPONDENCE between p-adics and reals

p-Adic number

x= SUM_(n>=n0) x_np^n

is mapped

to real number

y = SUM_(n>=n0) x_np^(-n)

Note that only the signs of powers of p are changed.

Second natural correspondence between p-adics and reals is based on the fact that both reals and p-adics are completions of rational numbers. Hence rational numbers can be regarded as common to both p-adic and real numbers. This defines a correspondence in the set of rationals. Allowing algebraic extensions of p-adic numbers, one can regard also algebraic numbers as common to reals and algebraic extensions of p-adics. p-Adic and real transcendentals do not have anything in common. Note that rationals have pinary expansion in powers of p, which becomes periodic for high pinary digits (predictability) whereas transcendentals have non-periodic pinary expansions (non-predictability). One could say that the numbers common to reals and p-adics are like islands of order in the middle of real and p-adic seas of chaos. Both correspondences are important in the recent formulation of p-adic physics.

G. p-Adic length scale hypothesis

p-Adic mass calculations force to conclude that the length scale below which p-adic effective topology is satisfied is given

L_p simeq R*sqrt(p), R= 10^4*sqrt(G) (CP_2 length scale).

('simeq' means 'in good approximation'). One has also good reasons to guess that p-Adic effective topology makes sense only above CP_2 length scale. One can also define n-ary p-adic length scales

L_p(n) =p^((n-1)/2)L_p

It is very natural to assume that the spacetime sheets of increasing size have typical sizes not too much larger than L_p(n). The following figure illustrates the situation.

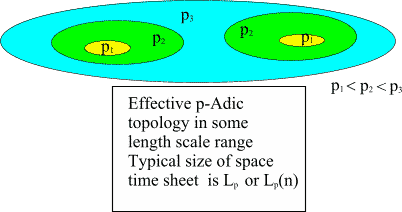
Fig. 22. p-Adic length scale hierarchy

The obvious question is 'Are there some physically favoured p-adic primes?'. p-Adic mass calculations encourage the following hypothesis

The most interesting p-adic primes p correspond to primes near prime powers of two

p simeq 2^k, k prime

Especially important are physically Mersenne primes M(k) for which this condition is optimally satisfied p= 2^k-1 Examples: M(127)= 2^127 -1, M(107) = 2^107 -1, M(89)= 2^89 -1: electron, hadrons, intermediate gauge bosons.

A real mathematical justification for this hypothesis is still lacking: probably the p-adic dynamics depends sensitively of p and this selects certain p-adic primes via some kind of 'natural selection'.

H. Generalization of spacetime concept

One can wonder whether p-adic topology is only an effective topology or whether one could speak about a decomposition of the space-time surface to real and genuinely p-adic regions, and what might be the interpretation of the p-adic regions (note that also real space-time regions would still be characterized by some prime characterizing their effective topology).

The development of TGD inspired theory of consciousness led finally to what seems to be a definite answer to this question. p-Adic physics is physics of cognition and intention. p-Adic non-determinism is the classical space-time correlate for the non-determinism of imagination and cognition. p-Adic spacetime sheets represent intentions and quantum jump in which p-adic space-time sheet is transformed to real one can be seen as a transformation of intention to action.

This forces to generalize the notion of the imbedding space. The basic idea is that rational numbers are in a well-defined sense common to both real number field R and all p-adic number fields R_p. The generalized imbedding space results when the real H and all p-adic versions H_p of the imbedding space are glued together along rational points. One can visualize real and p-adic imbedding spaces as planes, which intersect along a common axis representing rational points of H. Real and p-adic spacetime region are glued together along the boundaries of the real spacetime sheet at rational points.

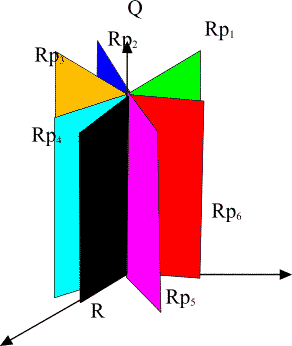
Generalized imbedding space is union of all p-adic imbedding spaces H_p and real imbedding space H intersecting along rational points common to all (Q denotes rationals, R for reals, and R_p for p-adic numbers). In figure some of the imbedding spaces H_p are illustrated as half-planes.

The construction of p-adic quantum physics and the fusion of real physics and p-adic physics for various primes to a larger scheme is quite a fascinating challenge. For instance, a new number theoretic view about information emerges. p-Adic entropy can be negative, which means that system carries genuine information rather than entropy.

Additional Illustrations

Spin Glass

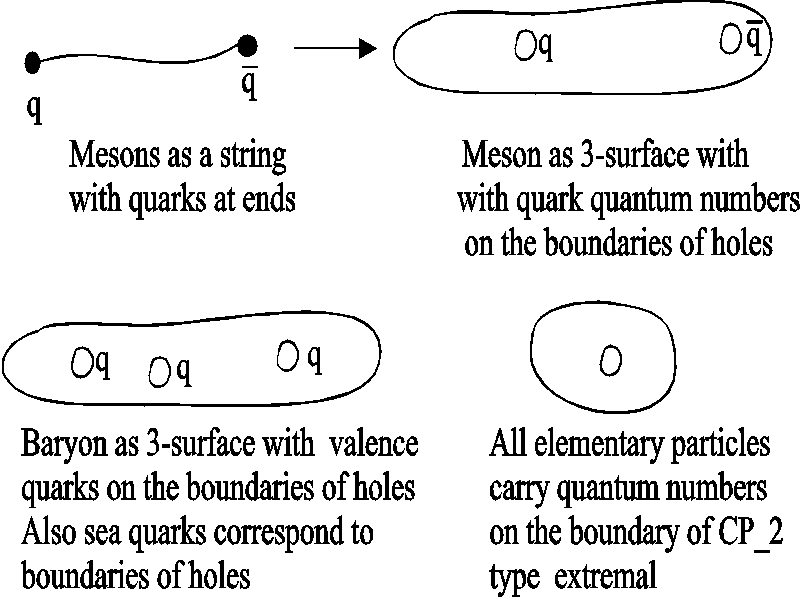
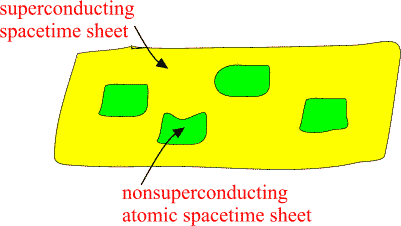
Atomic spacetime sheets are at high temperature and non-superconducting as standard physics predicts but larger spacetime sheets can have very low temperature and superconduct.